ModelFunction_PowerSpectrum_Angular.h File Reference

Global functions to model the angular power spectrum. More...

#include "Cosmology.h"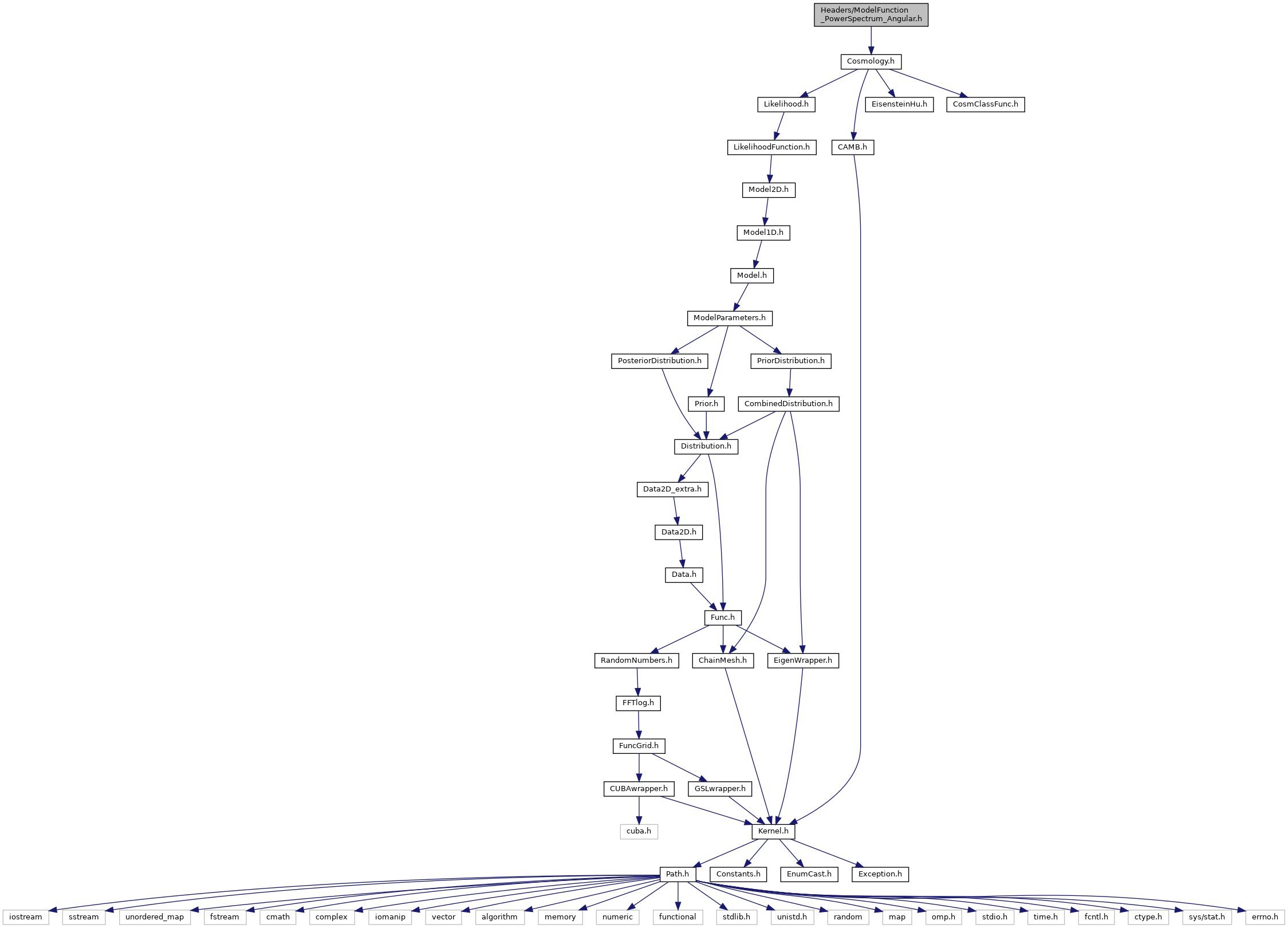

Include dependency graph for ModelFunction_PowerSpectrum_Angular.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Namespaces
	cbl
	The global namespace of the CosmoBolognaLib
	cbl::modelling
	The namespace of the functions and classes used for modelling

Functions
std::vector< double >	cbl::modelling::angularpk::Cl_mixed (std::vector< double > l_mixing, std::vector< std::vector< double >> mixing_matrix, std::vector< double > l, std::vector< double > Cl, double fsky)
	the angular power spectrum convolved with the mixing matrix More...
double	cbl::modelling::angularpk::integrand_limber_exact (double redshift, std::shared_ptr< void > pp, std::vector< double > par)
	the integrand function in the Limber approximation for the calculus of angular power spectrum More...
double	cbl::modelling::angularpk::integral_limber_interp (double l, std::vector< double > z_vector, std::vector< double > kk, cbl::glob::FuncGrid2D pk_interp, std::vector< double > parameter, std::shared_ptr< void > input)
	the integrand function in the Limber approximation for the calculus of angular power spectrum More...
double	cbl::modelling::angularpk::integral_limber_exact (double l, std::vector< double > parameter, std::shared_ptr< void > input)
	the integrand function in the Limber approximation for the calculus of angular power spectrum More...
std::vector< double >	cbl::modelling::angularpk::Cl_limber (const std::vector< double > l, const std::shared_ptr< void > inputs, std::vector< double > &parameter)
	the model for the angular power spectrum More...

Detailed Description

Global functions to model the angular power spectrum.

This file contains all the prototypes of the functions used to model the angular power spectrum

Author

Federico Marulli, Massimiliano Romanello

feder.nosp@m.ico..nosp@m.marul.nosp@m.li3@.nosp@m.unibo.nosp@m..it, massi.nosp@m.mili.nosp@m.a.rom.nosp@m.anel.nosp@m.l2@un.nosp@m.ibo..nosp@m.it

Definition in file ModelFunction_PowerSpectrum_Angular.h.

Function Documentation

Cl_limber()

std::vector< double > cbl::modelling::angularpk::Cl_limber	(	const std::vector< double >	l,
		const std::shared_ptr< void >	inputs,
		std::vector< double > &	parameter
	)

the model for the angular power spectrum

the model is the following:

\[ C_l = \frac{b^2}{N^2}\int_{0}^{\infty} \frac{dN}{dz}\frac{dN}{dz} P_{mat} \left(\frac{l+1/2}{r(z)}\right) \frac{H(z)}{c}\frac{1}{r^2(z)} dz\]

the model has n+3 parameters:

• \( n cosmological parameters, including \Omega_m, \Omega_b and \sigma_8 \)
• \( b \)
• \( offset \)
• \( slope \)

the angular power spectrum is computed using the input cosmological parameters

Parameters

l	the vector of multipoles at which the model is computed
inputs	pointer to the structure that contains the power spectrum angular data model
parameter	1D vector containing the linear bias and the offset and the slope of the normalized dN/dz distribution

Returns

the angular power spectrum in the Limber approximation

Definition at line 239 of file ModelFunction_PowerSpectrum_Angular.cpp.

Cl_mixed()

std::vector< double > cbl::modelling::angularpk::Cl_mixed	(	std::vector< double >	l_mixing,
		std::vector< std::vector< double >>	mixing_matrix,
		std::vector< double >	l,
		std::vector< double >	Cl,
		double	fsky
	)

the angular power spectrum convolved with the mixing matrix

the function computes:

\[C_l^{mixed}=\sum_{l'} R_{ll'}C_{l'}\]

Parameters

l_mixing	the vector of multipoles of the mixing matrix
mixing_matrix	the mixing matrix
l	the vector of multipoles of the power spectrum
Cl	the angular power spectrum
fsky	the fraction of sky covered by the survey

Returns

the angular power spectrum convolved with the mixing matrix

Definition at line 45 of file ModelFunction_PowerSpectrum_Angular.cpp.

integral_limber_exact()

double cbl::modelling::angularpk::integral_limber_exact	(	double	l,
		std::vector< double >	parameter,
		std::shared_ptr< void >	input
	)

the integrand function in the Limber approximation for the calculus of angular power spectrum

the function computes:

\[C_l = \frac{1}{N^2}\int_{0}^{\infty} \frac{dN}{dz}\frac{dN}{dz} P_{mat} \left(\frac{l+1/2}{r(z)}\right) \frac{H(z)}{c}\frac{1}{r^2(z)} dz\]

Parameters

l	the multipole at which angular power spectrum is computed
parameter	the list of parameters, containing the cosmological parameters and eventually the offset and slope of the normalized dN/dz distribution
input	pointer to the structure that contains the power spectrum angular data model

Returns

the integral of the angular power spectrum in the Limber approximation

Definition at line 206 of file ModelFunction_PowerSpectrum_Angular.cpp.

integral_limber_interp()

double cbl::modelling::angularpk::integral_limber_interp	(	double	l,
		std::vector< double >	z_vector,
		std::vector< double >	kk,
		cbl::glob::FuncGrid2D	pk_interp,
		std::vector< double >	parameter,
		std::shared_ptr< void >	input
	)

the integrand function in the Limber approximation for the calculus of angular power spectrum

the function computes:

\[C_l = \frac{1}{N^2}\int_{0}^{\infty} \frac{dN}{dz}\frac{dN}{dz} P_{mat} \left(\frac{l+1/2}{r(z)}\right) \frac{H(z)}{c}\frac{1}{r^2(z)} dz\]

Parameters

l	the multipole at which angular power spectrum is computed
z_vector	the redshift vector of the interpolation grid
kk	the k vector of the interpolation grid
pk_interp	the interpolation grid object
parameter	the list of parameters, containing the cosmological parameters
input	pointer to the structure that contains the power spectrum angular data model

Returns

the integral of the angular power spectrum in the Limber approximation

Definition at line 64 of file ModelFunction_PowerSpectrum_Angular.cpp.

integrand_limber_exact()

double cbl::modelling::angularpk::integrand_limber_exact	(	double	redshift,
		std::shared_ptr< void >	pp,
		std::vector< double >	par
	)

the integrand function in the Limber approximation for the calculus of angular power spectrum

the function computes:

\[\frac{1}{N^2}\frac{dN}{dz}\frac{dN}{dz} P_{mat}\left(\frac{l+1/2}{r(z)}\right) \frac{H(z)}{c}\frac{1}{r^2(z)}\]

Parameters

redshift	redshift
pp	pointer to the structure that contains the power spectrum angular data model
par	vector containing the input parameters

Returns

the integrand function of the angular power spectrum in the Limber approximation

Definition at line 153 of file ModelFunction_PowerSpectrum_Angular.cpp.